Zadanie z matematyki

20.11.2009

14:13

[1]

Mipari [ Senator ]

Zadanie z matematyki

Mam problem z takim zadaniem:
Dany jest punkt B = (-2;0) i prosta l: 4x-3y+32=0 przecinająca oś OX w punkcie M. T jest trójkątem o największym polu wśród trójkątów prostokątnych takich, że wierzchołek kąta prostego należy do odcinka BM, punkt B jest wierzchołkiem kąta ostrego, a trzeci wierzchołek należy do prostej l. Oblicz obwód tego trójkąta.

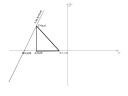
Narysowałem pomocniczy obrazek -->
Punkt M wyliczyłem podstawiając 0 pod y w równaniu prostej.
Żeby obliczyć obwód potrzebuję wszystkich współrzędnych. Domyślam się, że największe pole ten trójkąt będzie miał gdy |MA| = |AB|. I tu właśnie problem, bo tylko się domyślam, a nie wiem jak to udowodnić. Gdyby tak było to łatwo można by wyliczyć współrzędne punktu B i C. Więc moje pytanie brzmi: Kiedy pole tego trójkąta będzie największe i w jaki sposób można to udowodnić?

tomazzi [ Flash YD ]

To na pochodnych się robiło, zaraz sobie przypomnę jak.
A może i nie. Tak czy siak zaraz to rozwiążę :P
Odcinek BM może mieć długość (0,6). Wysokość trójkąta jest zależna od położenia punktu A.
-2-|AB| = Ax
Cy=h= (32+4*(-2-|AB|))/3
Teraz chyba robisz pochodną, szukasz ekstremów. Sprawdzasz pole trójkąta dla wartości w ekstremum oraz początku oraz końca przedziału (0,6).
Tak mi się wydaje to zadania tego typu miałem kilka lat temu.