 --> Archiwum Forum
--> Archiwum Forum
Matematyka. Zmienna losowa, gęstość, dystrybuanta...
Ogon. [ półtoraken fechten ]
Matematyka. Zmienna losowa, gęstość, dystrybuanta...
oo - nieskończoność
Zadanie robię na podstawie innego, trochę prostszego, więc nie do końca wszystko rozumiem.
Zmienna losowa X ma gęstość:
f(x)=
1/4 dla -2<x<0
Cx dla 1<x<2
0 dla pozostałych
I teraz gdy liczę dystrybuantę to:
1. dla x(-oo;-2):
całka od -oo do x z 0 = 0
(swoją drogą nie rozumiem czemu górna granica to 'x')
2. dla x(-2;0):
całka od 0 do x z 1/4 = 1/4x
3. i teraz przedział x(0;1):
nie wiem jaką tu całkę wstawić... ani jaki przedział, ani z czego ;/
4. dla x(1;2):
całka od 1 do 2 z Cx=3/2C
5. dla x(2; oo):
no i tu znowu nie wiem.
ew. może ktoś by miał jakoś po ludzku (pdf z wykładów mnie nie interesuje, bo wykłady po ludzku nie są) wytłumaczone w notatkach czy na jakiś forum to prosiłbym o linka...
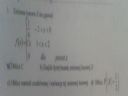
Ogon. [ półtoraken fechten ]
up
Ogon. [ półtoraken fechten ]
ostatni up przed jutrzejszym egzaminem ;P
Api15 [ dziwny człowiek... ]
Powodzenia!
Cainoor [ Mów mi wuju ]
Takie proste rzeczy - powinieneś się zwyczajnie nauczyć :)
Ogon. [ półtoraken fechten ]
Uczyć to się można było w semestrze... przypominanie sobie teraz tego po 3 miesiącach w stosie notatek to horror :(
Większość typów zadań już rozkminiłem, ale tego jednego nie mogę :(
...jesteście okrutni.
edit: znaczy Cainoor jest ;P
Ambitny Łoś [ Wielki Przedwieczny ]
Ja jutro mam ostatnią poprawkę z Analizy Danych i kompletnie nic nie umiem :( Za trudne to dla mnie jest i nawet nie wiem od czego zacząć.
_bubba_ [ Generaďż˝ ]
bo trzeba byc ambitnym, losiu!
Ogon. [ półtoraken fechten ]
Ja to zacząłem od zdobycia pytań...
zmudix [ Professor Fate ]
Od 0 do 1 mamy f(x)=0, więc całka też = 0. To samo dla x=(-oo,-2) oraz x=(2,oo).
Ogon. [ półtoraken fechten ]
A jak będzie dla 5) ?
Według tej logiki to:
całka od 2 do nieskończoności z zera = 0
tak?
Ale np w analogicznym zadaniu (tylko że jest przedział 1/4x^3 dla 0;2 i zero dla reszty) i
w ostatnim przedziale - od 2 do nieskończoności jest:
całka od 0 do 2 z (1/4t^3) dt = 1
...zupełnie bez sensu ;/
© 2000-2025 GRY-OnLine S.A.
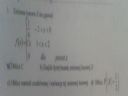
 --> Archiwum Forum
--> Archiwum Forum



