--> Archiwum Forum
lo0ol [ Jónior ]
Matma; prośba o sprawdzenie
Przekroj osiowy stozka jest trojkatem o P=144cm^2. Kąt nachylenia przy podstawie jest rowny 45 stopni. Oblicz objetosc i pole calkowite.
_______________
Na obrazku po prawej widoczne rozwiązanie kumpla. Moja wersja prezentuje trochę inne wyniki bo: V = 864 pi; P = 144 pi (1 + pierwiastek z 2). Zmiany spowodowane są tym, że u mnie r wyszlo 12, a u kumpla 6.
Mógłby ktoś podać prawidłowe rozwiązanie lub wskazać jedno z naszych? Z góry dzięki.
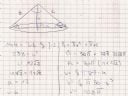
Belert [ Legend ]
r=12
aV2=12V2
a=12
a a to jest r i H .Amen :)
lo0ol [ Jónior ]
Dzięki Belert ... czyli tak jak myślałem. Doszło jeszcze jedno zadanie. Podobnie po boku kumpla, a moje wyniki to:
Pc = 24 pi + 48 pi pierwiastków z 3
V = 144 pi
Treść:
Walec, którego przekątna jest nachylona pod kątem 60(stopni).
Wysokosc 12cm. Oblicz pole calkowite i objętość.
ReproLit [ Centurion ]
lo0ol -> masz poprawne wyniki w zadaniu z [3]
kumplowi wyszedł za długi promień :)
Wydaje mi się, że niepotrzebnie użył wzoru na wysokośc trójkąta równobocznego, o wiele wygodniej to policzyć z tangensa kąta 60 stopni.
lo0ol [ Jónior ]
Jeszcze co do wypowiedzi Belerta:
czy aV2=12V2 jest dobrze?
Mi wyszło cuś a la obliczanie tej przeciwprostokątnej z twierdzenia Pitagorasa:
c^2 = V288 ^2 + V288 ^ 2
c = 24
ReproLit [ Centurion ]
Belert przez a oznaczył r, wszystko jest dobrze. Rozpatrywał połówke trójkąta.
edit: z Pitagorasa, jak widzisz również wynika, że r=12 (c=2r)
lo0ol [ Jónior ]
Czyli wynik pokazany na img dołączonym do posta [1] jest dobry czy ni? Z postu Belerta wynika,że a jest równe r. To przeczy temu, że a = 2r.
____
Edit: ahhhh sory cos popieprzyłem i byłem przekonany po powrocie do domu, że kilka godzin temu mi wyszło r=6. Nie ważne. :p
ReproLit [ Centurion ]
Wynik z obrazka jest błędny. Belert i twój kumpel zastosowali zupełnie inne oznaczenia.
U Belerta a=r=H.
Taka uwaga na przyszłość: WSZYSTKIE literki powinny być na obrazku, wtedy wiadomo co jest co.
edit: kurcze, sorry za bląd w [6], Belert założył oczywiście że a=r