 --> Archiwum Forum
--> Archiwum Forum
Kąty
Cros1sman [ Pretorianin ]
Kąty
Witam
Mam problem z katami opisanymi i wpisanymi. Kompletnie nie rozumiem kiedy np. odejmujemy od 180(stopni) iles tam, a kiedy od 360.
--> tutaj przykladowo mam obliczyc katy wewnetrzne, i pytanie ktore to sa, jak je dokladnie liczyc, czy sa na to jakies wzory.
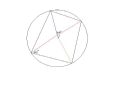
Kapitan Bomba @#$% [ Pretorianin ]
nie pamietam
|LoW|Snajper [ Senator ]
Jak masz np. 6 - kat czy cos to :
360 / 6 = 60
180 - 60 = 120 stopni
Loczek [ El Loco Boracho ]
Wszystkie trójkąty są równoramienne. Suma kątów w trójkącie to...? :)
Cros1sman [ Pretorianin ]
noo 180 :P
----> pozwolcie ze dam jeszcze jeden przykladowy. I co mam z tym zrobic krok po kroku, i piszcie (jesli mozecie) skad sie biore te liczby.
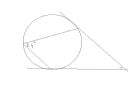
Kapitan Bomba @#$% [ Pretorianin ]
niezly rysunek
kali93 [ Isildur ]
Powiedz żebyśmy odrobili zadanie domowe za Ciebie tak będzie prościej:D
Cros1sman [ Pretorianin ]
nie mam zadania domowego. Tylko chce to umieć...
sliwonk [ wiem , beznadziejny nick ]
[5] jeśli to są styczne to
360-90-90-64=116 [stopni]
tworzy się deltoid o dwóch kątach 90 stopni, a wiadomo że suma kątów w każdym czworokącie wynosi 360 stopni
BTW 2 klasa gimnazjum? Dopiero tutaj? :d
DEXiu [ Generaďż˝ ]
sliwonk ==> Błąd. Deltoid będzie, jak połączy punkty styczności ze środkiem okręgu. Teraz to jest jakiś niezidentyfikowany czworokąt.
Cros1sman ==> Całą potrzebna wiedza:
- suma wszystkich trzech kątów w trójkącie wynosi 180 stopni
- suma wszystkich czterech kątów w czworokącie wynosi 360 stopni
- miara kąta środkowego (takiego, którego ramiona zawierają promienie okręgu; albo inaczej: takiego, którego wierzchołek pokrywa się ze środkiem okręgu) jest dwa razy większa od miary kąta wpisanego (takiego, którego wierzchołek jest na okręgu) opartego na tym samym łuku
- styczna do okręgu jest prostopadła (tworzy kąt prosty, tzn. 90 stopni) z promieniem tego okręgu poprowadzonym od środka do punkty styczności z tą styczną
Tyle. Bo tw. o mierze kąta między sieczną a styczną raczej nie mieliście. A metoda na rozwiązywanie tego typu zadań jest taka:
1. zrób rysunek
2. na rysunku zaznacz miary wszystkich kątów, które znasz
3. poszukaj, czy nie ma jakichś kątów wpisanych/środkowych opartych na tych samych łukach, a jeśli tak, to wylicz co się da i też zaznacz
4. sprawdź, czy nie można np. dorysować jakichś promieni okręgu tak, aby powstały wspomniane pary wpisany-środkowy; jeśli tak, to dorysuj, wylicz wszystko co się da i zaznacz
5. powtarzaj powyższe punkty tak długo, aż dojdziesz do rozwiązania
DEXiu [ Generaďż˝ ]
(sorry, edit się skończył)
Przykład (zadanie z postu [5]):
1. rysunek - jest
2. zaznaczyliśmy co wiemy - ok
3. kątów wpisanych i środkowych na tym samym łuku - na razie nie ma
4. dorysować coś - można. dorysowujemy promienie okręgu do punktów styczności ze stycznymi (od razu można zauważyć, że wtedy powstanie kąt środkowy oparty na tym samym łuku co wpisany, który już znamy - no to zaznaczamy i wyliczamy)
5. jeszcze raz:
1. jest
2. teraz zauważamy, że mamy dwa kąty między stycznymi a promieniami (które właśnie dorysowaliśmy) - zaznaczamy ich miary
3. pojawiła się para wpisany-środkowy (zauważyliśmy to już w punkcie 4. wyżej), więc jeśli jeszcze tego nie zrobiliśmy, to wyliczamy i zaznaczamy
4. nie za bardzo mamy co dorysować - na razie nic nie robimy, może wystarczy; jak się okaże, że utkwiliśmy w martwym punkcie to zaczniemy szukać co by tu sobie jeszcze pobazgrolić
5. jeszcze raz:
1. jest
2. zauważamy, że mamy czworokąt (ściślej - deltoid), w którym znamy miary trzech kątów - no i gitara; więcej do szczęścia nam nie potrzeba, bo możemy dzięki temu policzyć miarę czwartego kąta, który to jest szukany - KONIEC :)
Cros1sman [ Pretorianin ]
Dzieki DEXiu :) oswietliles troche moj mozg :P
:)
sliwonk [ wiem , beznadziejny nick ]
a to bardzo przepraszam, mój błąd
Cros1sman [ Pretorianin ]
No i po kilku "chwilach" glowkowania( o czym DEXiu do cholery pisze) rozgryzlem i katy w trojkatach i wielokatach. Wszystkim wielkie dzieki :) (szczegolnie DEXi'owi ktory rozjasnil troche moje myslenie)
© 2000-2025 GRY-OnLine S.A.


 --> Archiwum Forum
--> Archiwum Forum



