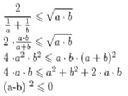--> Archiwum Forum
Masta5433 [ Pretorianin ]
Zadanie z matematyki
Możecie mi pomóc?
Mam taki jeden przykładzik z matmy:
2: (1:a+1:b) większe lub równe pierwiastek z ab
Polecenie brzmi: Wykaż, że dla dowolnych a,b,c należących do rzeczywistych zachodzi nierówność
jagged_alliahdnbedffds [ Rock'n'Roll ]
Gdzie tu jest 'c'?
Poczytaj o różnych rodzajach średnich - arytmetycznej, geometrycznej, kwadratowej i jeszcze jakaś tam była chyba...
Masta5433 [ Pretorianin ]
Ale jaki to ma związek z tym zadaniem, bo nie za bardzo jarzę
jagged_alliahdnbedffds [ Rock'n'Roll ]
Pierwsze wyrażenie to średnia harmoniczna, a drugie to średnia geometryczna...
edit. I tam powinno być chyba "mniejsze lub równe" zamiast większe lub równe.
Masta5433 [ Pretorianin ]
O_O jestem w pierwszej liceum i nie miałem jeszcze ani średniej harmonicznej, ani geometrycznej, może istnieje jakiś inny sposób, żeby to udowodnić?
I jest wyraźnie większe lub równe, zaraz zrobię zdjęcie zadanka
Masta5433 [ Pretorianin ]
Cholera, edit się skończył
Oto zdjęcie zadanka--->
Loczek--> wielkie dzięki :)
edit: jagged---> faktycznie :P
Loczek [ El Loco Boracho ]
2/(1/a+1/b)>=(a*b)^(1/2) , ab>0
2/((a+b)/ab)>=(ab)^(1/2)
ab/a+b >= (ab)^1/2
ab/((a+b)(ab)^(1/2))>=0
(ab)^(1/2)/(a+b)>=0 , a+b=((a+b)^2)^(1/2)
((ab)/((a+b)^2)^(1/2)>=0
ab>0 (założenie konieczne przy pierwotnej formie nierówności) i (a+b)^2>=0
Zamalowany Kwadracik :)
jagged_alliahdnbedffds [ Rock'n'Roll ]
To jak dla mnie w podpunkcie d) tam jest mniejsze lub równe ;]
Pokombinuj, bo to proste jest, a jak nic nie wychodzi to masz:
Tomuslaw [ Superbia ]
OK, Loczek mnie ubiegł :D
Chociaż... gdzie Ci wzięło dwójkę:
2/((a+b)/ab)>=(ab)^(1/2)
ab/a+b >= (ab)^1/2
oraz:
ab/((a+b)(ab)^(1/2))>=0 ??? Chyba powinno być >= 1 (jeśli dzielisz... albo to ja nie pojmuję ;)).
tomazzi [ Young Destroyers ]
Loczek - 2 po drodze zgubiłeś :) Ale rozwiązanie dobre :)
Loczek [ El Loco Boracho ]
Swoją drogą fakt o którym nie wspomniales (a>0 i b>0) skraca rozwiązanie do:
2/(1/a+1/b)>=(a*b)^(1/2) , ab>0
2/((a+b)/ab)>=(ab)^(1/2)
2ab/a+b >= (ab)^1/2
2ab/((a+b)(ab)^(1/2))>=0
2(ab)^(1/2)/(a+b)>=0
EDIT:o... czemu w książce jest <= skoro właśnie udowodniliśmy że jest >=??? Czy gdzieś zrobiłem błąd?
Tomuslaw [ Superbia ]
A tak w ogóle, to nierówność nie jest spełniona, bo dla a=4 i b=1 następuje:
2(0,25+1)>=2, CO JEST KOMPLETNĄ BZDURĄ :D
Zatem, od początku:
Uzależniamy a=f(b). Mamy zatem (przekształćcie sobie sami... lenie -.-):
-a + 2(ab)^0.5 - b <= 0
t^2 = a
-t^2 + 2b^0.5 * t - b <= 0
delta = 0, zatem istnieje tylko jedno rozwiązanie, a ponieważ współczynnik czy t^2 jest ujemny, więc spełnione jest dla każdego a i b, bo funkcja "ma ramiona skierowane do dołu i dla każdego a i b jest ujemna".
Edit: Loczek - tak, patrz mój post [9].
Loczek [ El Loco Boracho ]
mea culpa, pomyliłem sie... Tak to jest jak sie robi matme w edytorze postów GOLa :)
Tomuslaw [ Superbia ]
edit do postu [12] (koniec czasu):
więc spełnione jest dla każdego a i b, bo funkcja "ma ramiona skierowane do dołu i dla każdego a i b przyjmuje wartości ujemne lub równe 0."
jagged_alliahdnbedffds [ Rock'n'Roll ]
Jeju, to jest zadanie z 1 klasy LO - to nie jest takie trudne...
edit. W ostatniej linijce ma być (a-b)^2 => 0 większe lub równe!, czyli spełnione, bo każdy kwadrat czegoś ma taką własność :)
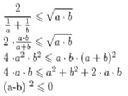
Masta5433 [ Pretorianin ]
[15] Nareszcie zrozumiałem :D I oto niezbity dowód, że GOL-owi eksperci od matmy nauczą cię lepiej, niż kiepski nauczyciel
Tomuslaw [ Superbia ]
Bo zrobili za Ciebie? Nie bądź śmieszny facet...
Masta5433 [ Pretorianin ]
Nie, nie dlatego, mam taką tragiczną nauczycielkę, że nawet to, co ona pisze na tablicy trudno zrozumieć, tymczasem tutaj jagged_alliahdnbedffds napisał wszystko jasno i przejrzyście i teraz wiem, gdzie robiłem błąd :P
jagged_alliahdnbedffds [ Rock'n'Roll ]
Tylko mi nie mów, że się nadaję na nauczyciela :P A na przyszłość - polecam jakieś stronki a'la Google do pomocy przy rozwiązywaniu zadań - zrozumiesz to, a nie tylko rozwiążesz jedno zadanie :)
Masta5433 [ Pretorianin ]
Szczerze mówiąc sądzę, że lepiej nauczyłbyś mnie matmy, niż moja nauczycielka, mówię poważnie.