Matematyka - zadanie

Łysy. [ Pretorianin ]

co to jest A=10? odcinki oznaczamy przez zdefiniowanie ich końców, czyli przez podanie dwóch punktów, np. AC, AB. Kąty zaś, oznaczamy przez podanie kolejno: punktu na jednym ramieniu, punktu przęcięcia ramion, i punktu na drugim ramieniu, nie ma więc czegoś takiego jak kąt C, tylko kąt ACB na ten przykład. Rozumiem, że można się domyśleć o co chodzi, alerowniedobrzemogezaczacpisacbezspacjiipolskichznakow. Chodzi o przejrzystość.

DEXiu [ Senator ]

Łysy --> Kwestia konwencji. Niekiedy można się spotkać z takim właśnie zapisem. W przypadku wielokątów zapis "kąt A" jest z reguły równoznaczny z "kąt wewnętrzny o wierzchołku A"; a co do odcinka, to często w trójkącie przyjmuje się oznaczenie np. a jako odcinek naprzeciw wierzchołka A itp. Ale generalnie masz rację, że "superpoprawnie" byłoby tak jak podajesz.
pajkul ==> Nie do końca tak. Możesz albo się babrać "naokoło" w tw. cosinusów, albo wprost - z tw. sinusów dostaniesz od razu promień okręgu opisanego i możesz wyliczyć pozostałe boki, a także pole - poprzez wzór, który podałeś, tylko "w drugą stronę" (nie wyliczasz R znając P, tylko P znając a, b, c i R :)

Api15 [ dziwny człowiek... ]

Najlepiej jak wkleisz z painta ten trójkąt :)

11.09.2010

22:21

[6]

Łysy. [ Pretorianin ]

A teraż, żeby Ci trochę pomóc:
Promień można policzyć z zależności:

2R=a/sin(alfa)=b/sin(beta)=c/sin(gamma) gdzie 'a' jest odcinkiem leżącym na przeciż kąta alfa itd.

Dalej sam pokombinuuj :)

pajkul [ Generaďż˝ ]

Mialo byc AC= 10

Łysy. [ Pretorianin ]

no to w takim razie z moich prostych obliczeń(mam nadzieję dobrych) R będzie wynosić 5 sqrt(2), 5 pierw. 2. Dalej musisz sobie pokombinować :)

pajkul [ Generaďż˝ ]

Znowu zapomnialem, ze w twierdzeniu sinusow tez jest mowa o promieniu okregu opisanego na trojkacie.

Teraz cos innego, na to juz nie mam zadnego pomyslu.

$ebs Master -> Chciales powiedziec rownanie koła, bo jest tam znak nierówności. Ale pomysl dobry, tylko nie mialem nigdy nic o kole w geometrii analitycznej.

update: Zrobione :)

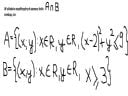
$ebs Master [ Profesor Oak ]

pajkul --> zbior A jest to rownanie okregu
zbior B to chyba sobie poradzisz, narysuj oba i zastosuj dzialanie na zbiorach

pajkul [ Generaďż˝ ]

Jeszcze jedno bardzo mnie męczy. Nie jestem pewien, czy mam odpowiednie wiadomosci do rozwiazania tego zadania, bo jakos nic mi nie przychodzi do glowy.

Liczby te sa kolejnymi wyrazami ciagu arytmetycznego. Oblicz x.

Logarytmow jeszcze nie mialem.

O_RLY -> rownan wykladniczych jeszcze nie mialem, ale juz wiem jak to zrobic. thx

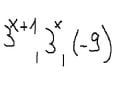
O_RLY [ Pretorianin ]

[11]pajkul

Skorzystaj z zależności, że wyraz środkowy ciągu arytmetycznego jest średnią arytmetyczną wyrazów sąsiednich.

3^(x+1) - 9 = 2 * 3^x

Rozwiązaniem powyższego równania jest x=2.

pajkul [ Generaďż˝ ]

A nie wie ktos przypadkiem, jak rozwiazac takie nierownosci?:

sin x - 2 cos x = 1

sin x + cos x = 1

w przedziale (-pi, pi)

tomazzi [ Flash YD ]

[11] To co dał O_RLY to nie równanie wykładnicze:
3^(x+1) - 9 = 2 * 3^x
3*3^x- 2*3^x = 9
3^x = 9
3^x = 3^2
x=2

Edycja: Chociaż może to i pod wykładnicze podlega. Nie myślę już.

DEXiu [ Senator ]

pajkul, co ty się do matury przygotowujesz czy co? Taki rozrzut materiału w tak krótkim czasie? :/ Chyba że macie jakąś powtórkę materiału z zeszłych lat, a przez całą wcześniejszą matematyczną edukację (ewentualnie całą poprzednią klasę) dawałeś szarym komórkom odpocząć :]

Co do postu [13] to nie nierówności tylko równania - mam nadzieję, że wiesz na czym polega różnica pomiędzy jednym a drugim. Rozwiązać możesz na przykład wykorzystując "jedynkę trygonometryczną": (sin x)^2 + (cos x)^2 = 1

pajkul [ Generaďż˝ ]

Czy to jest dobrze? Bo cos wynik jest malo przyjemny.