GOL'owy kalkulator, czyli - Matematyka - Królowa wszystkich nauk. Cz.2

jagged_alliahdnbedffds [ Rock'n'Roll ]

A kto Ci na weekendzie będzie matme rozwiązywał? :P

lajtowy ziomek:) [ God of War ]

jagged_alliahdnbedffds---> Takiego komenta bym się spodziewał po osobie o małym stażu na forum, no ale osoba mająca 50 level!? Po co to w ogóle piszesz człowieku? Nie umiesz przeczytać wstępniaka, gdzie w regulaminie wyraźnie pisze: "Piszemy tutaj tylko i wyłącznie zadania matematyczne (czyt. nie zbaczamy na na tematykę innych przedmiotów itd.) oraz odpowiedzi na konkretne np. równanie."
Ten wątek został utworzony z myślą aby pomagać innym, a to, że nikt nie zwróci się o pomoc w rozwiązaniu zadnia w weekend, to ok, da się zrozumieć. Niemniej na przyszłość oszczędź sobie takie nic niewnoszące komentarze.:P

Koniec offtopa. Jak ktoś ma jakieś zadanka, to śmiało, będziemy radzić.:)

jagged_alliahdnbedffds [ Rock'n'Roll ]

A tam się spinasz niepotrzebnie ;)

Dobra, to mam zadanie z egzaminu:

Udowodnij, że dla każdego x>0, ln(1+x) > (arctgx)/(1+x)

lajtowy ziomek:) [ God of War ]

jagged_alliahdnbedffds---> No i właśnie temu ma służyć ten wątek.:) Z tym, że ja osobiście jestem na poziomie matmy II klasy liceum (klasa human.), także nie jestem pewien czy ten materiał już brałem...;P No ale pamiętajmy, że ten wątek na tym polega, że gdzie jeden ma za małą wiedzę żeby pomóc, tam drugi podoła (dosłownie i w przenośni) zadaniu.;)

Edit: Co do zadania, to jeśli: dzielisz przez (x+1) i zakładając, że druga liczba pod drugiej stronie (arctgx) jest zerem, to otrzymujesz wynik:

Czyli fałsz. Tak więc mój tok rozumowania chyba nie jest tutaj należyty...;P

Jeckyl [ Nieuk ]

[5]



[6]

Jak dzielisz przez (x+1)? Wytłumacz mi co ma Ci to dać.

lajtowy ziomek:) [ God of War ]

Jeckyl---> Teraz już wiem, że to był absolutnie błędny "trop"...;P

lajtowy ziomek:) [ God of War ]

"Up" porządkowy...

lajtowy ziomek:) [ God of War ]

Miałem poczekać do końca tygodnia z podniesieniem wątku ale widzę, że zapomniano do czego służą wątki cykliczne o określonej tematyce.;P
Zachęcam do powierzania swych zadań GOL'owym matematykom.
Pozdrawiam.

kajtek603 [ International Level ]

Witam mam takie zadanie

Naszkicuj wykres funkcji y=|f(x)| x e R. Podaj dziedzinę, zbiór wartości oraz miejsce zerowe f i y=|f(x)|.
a)f(x)=-2x+1

No i mam pytania czy na wykresie tak p=-2 w dol i p=1 w lewo ?

lajtowy ziomek:) [ God of War ]

kajtek----> poczekaj chwilkę zaraz dam Ci wynik w spoilerze. Masz Szczęście bo właśnie co przerabiam funkcje.;)

Edit: kajtek---> czyli-->

Jeśli przesuwasz o (-2;1) to wygląda to tak: najpierw przesuwasz wykres o dwie jednostki w lewo, następnie jedną w górę i nanosisz na ten (wykres) te poprawki.
Jeżeli zaś masz układ (1;-2) to, najpierw jedną jednostkę w prawo, następnie dwie w dół...

No i pamiętaj, aby uzyskać punkty do narysowania wykresu rysujesz tabelę, na zasadzie x/y, za "x" podstawiasz dowolną liczbę. Przykład: x = -1, wówczas y = 3, ponieważ -2 * -1 = 3, to jest już jeden punkt na wykresie (-1;3), analogicznie znajdź w ten sposób pozostałe...

kajtek603 [ International Level ]

lajtowy ziomek:)----> thx już wiem jak zrobić.

Mam jeszcze problem z tym zadaniem:
Wykorzystując wykres funkcju f(x)=x^3+3, x e R, naszkicuj wykres funkcji y=|f(x)| oraz y=(|x|).

Więc mam narysować tabelkę ?, bo w odpowiedzi mam przesunięcie u=[6,0] i u2=[0,-3] i nie wiem jak je obliczyć.

lajtowy ziomek:) [ God of War ]

Spóźniony "Up" nowo tygodniowy...

lajtowy ziomek:) [ God of War ]

Chyba ostatni "Up" tego wątku, ostatni, bo nikt się nie udziela, a szkoda, ponieważ początki były obiecujące...;P Jeśli w przeciągu tygodnia nikt się nie będzie udzielał (na temat opisany we wstępniaku ofc), to wątek będzie do zamknięcia...

Arxel [ Kostka Rubika ]

Zadania:


Pierwsze:

?? Brak zastosowania któregokolwiek kryterium trochę mnie zdziwił.. To jedyne co mi przyszło do głowy..

Macierz: nieskończenie wiele rozwiązań zależnych od jednego parametru?

Royal_Flush [ Generaďż˝ ]

Dzisiaj na maturze miałem trzy zadanie i szczerze powiem że nie wiedziałem jak je zrobić :/

1) mamy podany prostokąt i udowodnić że punkty dwusiecznych kątów wewnętrznych po przecięciu będą wierzchołkami kwadratu.

2) jest funkcja y=f(x) i jej wierzchołek to (1;-9) i parabola przechodzi przez punkt (2,-8) i trzeba było napisać wzór funkcji kanonicznej i obliczyć miejsca zerowe i wykres.

3) jest trójkąt prostokątny o środkowym boku 8 i jego boki tworzą ciąg geometryczny. Obliczyć pole i promień okręgu opisanego na tym trójkącie.
--------------------------------------------------------------------------------------------------------

1) nie zrobiłem bo nie wiem co o dwusieczna. :/

2) no mają wierzchołek wychodzi że p=1 a q=-9 i mogłem wyliczyć a z kanonicznej podstawiając pod y=-8 i pod x=2 wyszło a potem obliczyłem b i c miejsce zerowe i mi nie wyszła parabola tylko jakieś powyginane cuś ;/ i c mi wyszło -8 czyli punk przecięcia z osią y jest w tym punkcie ale y równe -8 daje x=2 :/ i dupa :/

3) kurwa co ja zrobiłem to masakra *_* ja pierdole jestem zjebem na 110% *_* kurwa teraz to zauważyłem *_*
bo zrobiłem sobie że (8-r)2 + 8^2 = (8+r) i kurwa tu są wzory skróconego mnożenia.. jaka porażka nie zauważyłem , ale wstyd kurwa co za hańba :/ LOL kuuurwa jaki wstyd same 5 mama a takiego czegoś nie umiem. kurwa jaki żal wstydzę się :( idę się upić :/

Filevandrel [ czlowiek o trudnym nicku ]

AD 1
dwusieczna - Jak dorwe skaner to sie postaram wrzucic namalowane rozwiazanie

AD2

korzystając z wierzchołka

f(x)=a*(x-1)^2 -9

korzystająć z punktu (2,-8)

-8=a*(2-1)^2 -9
-8=a*(1)^2 -9
-8=a-9
a=1

f(x)=(x-1)^2 -9
f(x)=x^2 -2x -8

d=b^2 - 4ac= 4 - 4*(-8) = 36
sqrt(d)=6

x1=4
x2=-2

sprawdzamy czy wierzcholek jest ich srednia arytmetyczna->

1=(4-2)/2
1=2/2
1=1
czyli te wyniki moga być pierwiastkami

zwracam uwage na to ze to sprawdzenie nie daje pewnosci czy otrzymany wynik jest dobry, 1 jest tez srednia arytmetyczna np liczb 2 i 0, ale gdyby w ostatnim rownaniu wyszla mi sprzecznosc wynik bylby na 100% zly.

3)
"i jego boki tworzą ciąg geometryczny"

(8-r)2 + 8^2 = (8+r) -> ciąg arytmetyczny
a, a*q, a*q^2 .... itd -> ciąg geometryczny

Jaki ostatecznie ma byc ten ciąg?

Royal_Flush [ Generaďż˝ ]

arytmetyczny czyli boki są 6,8 i 10

AD 2 ale też zrobiłem tak jak ty i mi wyszła jakaś powyginana ta parabola ;/

Filevandrel [ czlowiek o trudnym nicku ]

jeżeli zrobiłeś tak jak ja i wyniki otrzymałeś takie same to problem wystąpił gdzies na etapie rysowania.

Może to Ci pomoże



Generalnie polecam wolframalpha. Może sie przydac w nauce do matury.

I zdradź mi jeszcze jedną rzecz- to są zadania z matury podstawowej prawda?

Royal_Flush [ Generaďż˝ ]

tak tak

jagged_alliahdnbedffds [ Rock'n'Roll ]

[17] :: Dwusieczna kąta - jak sama nazwa wskazuje - jest to prosta, która siecze kąt na dwa kąty o równej mierze.


1) Szkicujesz rysunek i korzystasz z tego, że dwusieczna kąta jest zbiorem punktów równo odległych od ramion tegoż kąta.


2) Jeśli wierzchołek to punkt W=(1,-9), to podstawiając te współrzędne do postaci kanonicznej paraboli y=a(x-p)^2+q, gdzie W=(p,q), otrzymamy wzór z trzema niewiadomymi x,y,a. Teraz podstawiając za (x,y) współrzędne punktu P=(2,-8), przez który przechodzi parabola, wyliczymy a i wstawiając do poprzedniego wzoru mamy postać kanoniczną tej funkcji.

Przyrównując funkcję do zera, obliczamy miejsca zerowe (będą albo 2 albo 0, bo jedno byłoby tylko wtedy, gdy wierzchołek leżałby na osi OX).

3) Boki tworzą ciąg arytmetyczny, czyli 2y = x+z (gdzie x,y,z - boki trójkąta). W Twoim zadaniu y=8, więc x+z=16. Jeśli okrąg jest opisany na trójkącie prostokątnym, to przeciwprostokątna (najdłuższy bok, czyli z) jest średnicą tegoż okręgu. Tak, więc promień, będzie połową długości przeciwprostokątnej trójkąta. Pole okręgu: P=pi*R^2.

W [19] piszesz, że, jeśli ciąg jest arytmetyczny i środkowy bok wynosi 8, to pozostałe dwa równają się 6 i 10, co jest nieprawdą, bo różnica ciągu arytmetycznego nie zawsze wynosi 2 (a jeśli w tym wypadku tak jest, to nie napisałeś tego w treści zadania).




BTW, jak będziesz pił, to staniesz się głupszy, a nie mądrzejszy ;)

Royal_Flush [ Generaďż˝ ]

W [19] piszesz, że, jeśli ciąg jest arytmetyczny i środkowy bok wynosi 8, to pozostałe dwa równają się 6 i 10, co jest nieprawdą, bo różnica ciągu arytmetycznego nie zawsze wynosi 2 (a jeśli w tym wypadku tak jest, to nie napisałeś tego w treści zadania).

ale to wyliczyłem bo:
(8-r)2 + 8^2 = (8+r) czyli (64-16r+r2)+64 = 64+r2+16r czyli wychodzi r=2
że tylko ja nie zauważyłem wzorów i napisałem 64+r2 + 64 = 64 - r2 - ale wstyd :/

jagged_alliahdnbedffds [ Rock'n'Roll ]

[16] :: Na razie tylko tyle ;)

2) f(x) = x * ln^2(x)


Dziedzina
x > 0


Przeciwdziedzina
x - zawsze dodatni, lnx może przyjmować wartości ujemne, ale jest do kwadratu, więc y >= 0


Ekstrema
I pochodna:
f'(x) = 1 * ln^2(x) - x * 2ln(x)/x = ln^2(x) - 2ln(x)
f'(x) = 0 <=> ln^2(x) - 2ln(x) = 0
ln(x) * (ln(x) - 2) = 0
ln(x) = 0 lub ln(x) = 2

x = 1
x = e^2


f'(x) > 0 <=> ln(x) * (ln(x) - 2) > 0

0<x<1 lub x>e^2 - dla tych x'ów funkcja jest rosnąca


f'(x) < 0 <=> ln(x) * (ln(x) - 2) < 0

xe(1,e^2) - dla tych x'ów funkcja jest malejąca


Analizując powyższe rozwiązania
Min x = 1, wynosi f(x) = 0
Max x = e^2, wynosi f(x) = 4e^2


3) AX=Y, gdzie A=((2, 1, 1),(1, 2, -1),(-2, -1, -1)), X=((x, y, z)), Y=((4, 3, 1))
detA = -4 + 2 - 1 + 4 - 2 + 1 = 0, więc korzystamy z Twierdzenia Kroneckera-Capellego.


B=((2, 1, 1),(1, 2, -1),(-2, -1, -1),(4, 3, 1))
rzA = 2 = rzB, więc układ posiada nieskończenie wiele rozwiązań, zależących od (3-2=1) jednego parametru.


Po obliczeniach: x-z = 5/3, y = 2/3, więc podstawiając alfa = z, otrzymujemy
X=((5/3+alfa, 2/3, alfa)) <=> X=((5/3, 2/3, 0), alfa(1,0,1))
Jak widać rozwiązanie zależy od jednego parametru alfa.

BeneQ junior [ gt: Adrianeo pl ]

a ja mam takie zadanie.

Długość 2 boków trójkąta to 1 i 4 a miara kąta pomiędzy nimi wynosi 60 stopni.Oblicz promienie okręgów opisanego i wpisanego w ten trójkąt.

jagged_alliahdnbedffds [ Rock'n'Roll ]

[25] :: Twierdzenie sinusów i wzór na promień okręgu wpisanego w trójkąt.

lajtowy ziomek:) [ God of War ]

"Up" na nowy tydzień.

lajtowy ziomek:) [ God of War ]

Up...

lajtowy ziomek:) [ God of War ]

Podniesienie wątku na nowy tydzień...

Krol Pawel [ Among the net ]

Jak to rozwiązać ?

a^2 + b^2 + 5 => 2a + 4b
(większe lub równe)

DEXiu [ Senator ]

Krol Pawel ==> Przenosisz wszystko z prawej strony na lewą, zwijasz w sumę dwóch kwadratów (być może trzeba będzie coś dodać/odjąć) i to, co zostanie, przenosisz na prawo. Powstanie nierówność opisująca część płaszczyzny znajdującą się na zewnątrz pewnego okręgu (wraz z tym okręgiem) lub całą płaszczyznę (pomyśl w jakim przypadku). Tak na marginesie, to "większe lub równe" zapisuje się przeważnie tak: >=. A druga sprawa - albo nie było cię na lekcji (obecność ciałem a nie myślami także uważam za nieobecność :P ), albo jeszcze tego nie przerabialiście, albo najzwyczajniej w świecie za mało ćwiczyłeś, bo taka postać od razu powinna ci narzucać skojarzenie z równaniem okręgu (tutaj akurat jest nierówność, ale co do meritum nic się nie zmienia)

lajtowy ziomek:) [ God of War ]

Jako, że ostatnimi czasy ponownie zapomniano do czego służy owy wątek, czego efektem jest multum nowych wątków po 8 postów praktycznie każdy, postanowiłem omawiany wątek podnieść...

hopkins [ Zaczarowany ]

https://forumarchiwum.gry-online.pl/S043archiwum.asp?ID=10144780&N=1 Pomoze ktos?

lajtowy ziomek:) [ God of War ]

"up" porządkowy.

PS. Dawno się nikt tu nie wypowiadał, czyżby wszyscy nagle zaczęli rozumieć matmę.;)

Azerko [ Alone in the wild ]

ja dostałem 2 z testu :) więc uważam się za "króla" matmy :p

jagged_alliahdnbedffds [ Rock'n'Roll ]

Ja jak dostałem 2 (na studiach, btw. z których mnie potem wywalili), to już się takim królem nie czułem ;)

Azerko [ Alone in the wild ]

na razie jestem w I LO to do 3 będę się cieszył 2 a potem no cóż... zobaczy się ;)

lajtowy ziomek:) [ God of War ]

Ekhm, panowie łamiecie regulamin tego wątku, rozumiem chęć dyskusji ale na prawdę nie to jest w zamierzeniu istotą tego wątku...;P

jagged_alliahdnbedffds [ Rock'n'Roll ]

Dawać jakieś zadania, to rozwiążemy ;)

Filevandrel [ czlowiek o trudnym nicku ]

Ja zawsze chętnie pomogę tylko proble jest taki, że nieczęsto zaglądam na forum. Jak coś to pisać na mail/gadu :)

mozecie mnie dorzucic na jakas liste we wstepniaku z adnotacja ze sprawdzam codziennie i dosc czesto maila


[email protected]

lajtowy ziomek:) [ God of War ]

Filevandrel----> Jasne, jak tylko wroce do domku to Cie wpisze do wstepniaka wraz z odpowiednim przypisem.

Gersiak [ Centurion ]

Zadanie z matematyki:
Oblicz pole powierzchni graniastosłupa prostego, którego krawędź boczna ma 20 cm a podstawa jest :

a]trapezem rownoramiennym o bokach 10cm,6cm,4cm,4cm
b]rombem o przekatnych 12cm i 16 cm
c]trapezem rownoramiennym o podstawach 3 cm i 9 cm oraz wyskosci 4 cm

Zalezy mi tez o rysunku siatki romba. Robie i caly czas mi nie zgadzaja sie wyniki. Wyniki to :

a]32(15 + pierwiastek z 3)cm kwadratowych w przyblizeniu 535,4 cm kwadratowe
b]992cm kwadratowe
c]488 cm kwadratowe

lajtowy ziomek:) [ God of War ]

Ostatni (najprawdopodobniej) "up" tego wątku, a szkoda... szkoda, ponieważ miałem nadzieję, że będzie służył nam wszystkim (no i nawet przez pewien czas tak było;P), no ale jednak i tak inni użytkownicy tworzą odrębne wątki o tej tematyce umieszczając zazwyczaj jedno zadanie, choć mają możliwość umieszczenia go w stosownym wątku i tam się z nim uporać...

preDratronIX [ Generau ]

Mam problem z zadaniem.

"Czy do pudełka o wymiarach 6,3x9,5x17 [cm] można wlać mleko 1-litrowe? Przyjmij że grubość ścianki ma 0,5 mm."

Właśnie nie wiem o co chodzi w drugiej części zadania?

Może mi ktoś wytłumaczyć? (2 klasa gim, nauczyciel do dupy...)

Montera [ Michael Jackson zyje ]

preDratronIX ->

Korzystasz ze wzoru na objętość graniastosłupa V = abc

a = 6,3 b = 9,5 c = 17

1 L = 1 dm3 = 1 x (10 cm)3 = 1000 cm3

V = 1017,45 cm3

1 L = 1000 cm3

Można od razu obliczyć odejmując od każdego rozmiaru 5 mm.

5 mm = 0,5 cm

6,3 cm - 0,5 cm = 6,25 cm
9,5 cm - 0,5 cm = 9,45 cm
17 cm - 0,5 cm = 16,95 cm

i wtedy 6,25 x 9,45 x 16,95 = 1001,11 cm3

Jak widać, zmieści się.

preDratronIX [ Generau ]

Montera. W odpowiedziach pisze że "NIE", a grubość ścianki wynosi 0,5 mm.

Czytaj ze zrozumieniem.

jagged_alliahdnbedffds [ Rock'n'Roll ]

6,3 cm - 0,5 cm = 6,25 cm
9,5 cm - 0,5 cm = 9,45 cm
17 cm - 0,5 cm = 16,95 cm

Wow, interesujące ;)


Montera. W odpowiedziach pisze że "NIE", a grubość ścianki wynosi 0,5 mm.
Czytaj ze zrozumieniem.

Trzeba odjąć po prostu po 2 * 0,5 mm z każdego wymiaru i wtedy objętość wyjdzie zapewne mniejsza niż 1000 cm^3.

Wyszło mi:

jagged_alliahdnbedffds [ Rock'n'Roll ]

Zadanie z matematyki:
Oblicz pole powierzchni graniastosłupa prostego, którego krawędź boczna ma 20 cm a podstawa jest :

a]trapezem rownoramiennym o bokach 10cm,6cm,4cm,4cm
b]rombem o przekatnych 12cm i 16 cm
c]trapezem rownoramiennym o podstawach 3 cm i 9 cm oraz wyskosci 4 cm

Zalezy mi tez o rysunku siatki romba. Robie i caly czas mi nie zgadzaja sie wyniki. Wyniki to :

a]32(15 + pierwiastek z 3)cm kwadratowych w przyblizeniu 535,4 cm kwadratowe
b]992cm kwadratowe
c]488 cm kwadratowe


Pisząc pole powierzchni nie masz zapewne na myśli 'pola powierzchi bocznej', nie? Bo jeśli o nią chodzi, to w a) nie ma szans, żeby z liczb 20, 10, 6, 4 wyszły jakieś pierwiastki.
Napisz dokładnie co trzeba obliczyć, bo to proste wzory są na wszystko przecież.


edit. Wyniki zgadzają się, jeśli obliczymy pole powierzchni całkowitej :)

lajtowy ziomek:) [ God of War ]

Uprzejmie proszę o pomoc w rozwiązaniu zadania z działu: "Okrąg i Koło". Oto ono:
Dwa przeciwległe wierzchołki kwadratu ABCD to punkty A=(3;-2) i C=(-1;2). Napisz równanie okręgu wpisanego i okręgu opisanego na tym kwadracie.

Bardzo dziękuje za pomoc.

lajtowy ziomek:) [ God of War ]

Up, drodzy GOL-owi matematycy.:)

Macco™ [ Child Of The Damned ]

lajtowy---> Nie mam za wiele czasu więc w liczenie się bawił nie będę ale tak pobieżnie:

-równanie okręgu ma postać x-xs)^2+(y-ys)^2=r^2 - x, y to punkty leżące na okręgu, xs, ys to współrzędne środka okręgu

-do podania równania okręgu opisanego na kwadracie należy podstawić współrzędne dwóch wierzchołków i zrobić układ równań i powinno wyjść

-do obliczenia równania okręgu wpisanego w kwadrat możesz np. obliczyć współrzędne środków dwóch boków równoległych i zastosować tą samą metodę co przy okręgu opisanym - do tego podpunktu możesz sobie zrobić rysunek żeby CI było łatwiej

No i to tyle bo na więcej nie mam czasu :)

lajtowy ziomek:) [ God of War ]

Macco---> Dzięki wielkie, Twoja pomoc okazała się mi bardzo przydatna.:)

kubomił [ Legend ]

Ok, jest problem. Liczę na Waszą na pomoc, mianowicie.

Mógłby mi ktoś wytłumaczyć dlaczego Pp (pole podstawy) graniastosłupa prawidłowego trójkątnego wyniosło pierwiastek z 3? (przy dł. krawędzi podst. 2cm oraz dł. kr. bocznej 5 cm)

------------------------------------------------
Podstawiłem do wzoru na trójkąt (1/2a*h) i dupa. Robiłem z Tw. Pitagorasa - warmer, ale nadal to nie to...

Macco™ [ Child Of The Damned ]

kubomił ---> raniastosłupa prawidłowego trójkątnego - to sugeruje, że trójkąt jest równoboczny a więc wystarczy zastosować wzór (a^2sqrt3)/4

kubomił [ Legend ]

Macco - dokładnie, podstawiłem zły wzór :) a to jednak nie jest takie trudne jak się sądzi :P

Sitros [ The One ]

Intryguje mnie jedno zadanie z trygonometrii... Nie jest to obowiazkowe lecz jednak chcialbym je zrozumiec. Jezeli ktos ma pomysl jak je zrobic to zapraszam.

Wykaż że jeśli a, b, y są kątami trójkąta, to
Sina + sinb + siny = cosa/2cosb/2cosy/2

(Slash to kreska ulamkowa)

a - kat alfa
b- kat beta
y - kat gamma

lajtowy ziomek:) [ God of War ]

Sitros---> Na razie się bliżej temu nie przyglądnąłem ale na pierwszy rzut oka stwierdzam, że należy tutaj skorzystać z własności trygonometrycznych, w tym min. z jedynki trygonometrycznej. Z tym, że nawet na pierwszym spojrzeniu jakoś nie dostrzegam tutaj tegoż triku.;) Może by tak pokombinować nimi, poprzekształcać je... hmmm... zaintrygowało i mnie to zadanko, jutro je postaram się zrobić, a mniemam, że nie zależy Ci specjalnie na czasie.:)

jagged_alliahdnbedffds [ Rock'n'Roll ]

^

Ja mogę dodać, że na pewno pożyteczna jest informacja, że są to kąty trójkąta (np. można pozbyć się trzeciego kąta 'y' przez zamienienie go na '180 - (a+b)').

U-boot [ Karl Dönitz ]

Witam

mam problem z pewnym zadaniem z 3 klasy gimnazjum,

oto one:
Mama gotuje zaprawy na zime w garnku o srednicy 24 cm
Czy zmiesci sie w tym garnku 8 sloikow o srednicy 8 cm, ustawiajac sloiki tylko w jednej warstwie ?
graficzne rozwiazanie pokazuje, ze mozna jednoczesnie wsadzic tylko 7 sloikow,
ale w jaki sposob rozwiazac, udowodnic to analitycznie ??

ma ktos jakis pomysl ?

z gory dziekuje za wszelakie sugestie

Pozdrawiam

irenicus [ Mareczek ]

budując sześciokąt, czy co tam wyjdzie, ze średnic słoików

U-boot [ Karl Dönitz ]

irenicus --> moglbys rozszerzyc swoja wypowiedz ?

zbuduje szczesciokat i ... ?

Pozdrawiam

U-boot [ Karl Dönitz ]

^^ up ?

irenicus [ Mareczek ]

Dobra, może to było zbyt ogólne... a do tego błędne :)

Rysunek --> dobra kartka się zagięła... ale ideę widać :)

Budujemy trójkąt równoboczny na promieniach dużego okręgu, wipsujemy w ten trójkąt okrąg, a teraz korzystamy z naszych umiejętności matematycznych i obliczamy promień tegoż okręgu wpisanego, wychodzi nam 8...
Czyli jak podzielimy resztę garnka na 6 części powstanie 6 trójkątów (to jest teraz szeciokat który mnie oswiecil). Wniosek, na pewno mieści się 6 słoików. Teraz jeszcze tylko musisz udowodnić, że do środka wejdzie tylko jeden i po zadaniu... Całkiem trudne jak na gimnazjum :)

Glob3r [ Tots units fem força ]

Mógłby ktoś pomóc to rozwiązać? To znaczy, niby to bez żadnego problemu rozwiązałem, ale prawidłowe odpowiedzi wskazują odpowiedź inną od mojej.

jagged_alliahdnbedffds [ Rock'n'Roll ]

^
1 2 2 2 2 3 3 4 4 4 4 5 5 5 5 6 6 6 6 6 6 6 6

Wszystkich 23, więc szukamy 12. oceny - jest to 5. Odp. B

irenicus [ Mareczek ]

Aby obliczyć medianę ze zbioru n obserwacji, sortujemy je w kolejności od najmniejszej do największej i numerujemy od 1 do n. Następnie, jeśli n jest nieparzyste, medianą jest wartość obserwacji w środku.

Czyli twoją medianą będzie wynik numer 12 :) B. 5

Edit... czemu ja się 21 doliczam? >_< racja... a już wiem... bo z ostatniej kolumny dodałem wynik a nie ilośc wyników ^^

U-boot [ Karl Dönitz ]

irenicus --> dziekuje, za dotychczasowa pomoc, jednak mam pewne watpliwosci, tzn dwa pytania

pierwsze pytanie
napisales:
Budujemy trójkąt równoboczny na promieniach dużego okręgu, wipsujemy w ten trójkąt okrąg
patrzac na rysunek, mamy co prawda trojkat zbudowany zgodnie z instrukcja powyzej, jednak okrag jest juz wpisany w inny trojkat

moje drugie pytanie wiaze sie z uniwersalnoscia Twojego rozwiazania:
co by bylo, gdyby byla inna srednica ? na przyklad 4 cm ? w jaki sposob wtedy budowalo by sie trojkat ??

Pozdrawiam

irenicus [ Mareczek ]

Nie rozumiem pytań :D

ad. 1 Masz duży pogrubiony trójkąt równoboczny, widać? ok
Ten okrąg, którego... ściany(?) są styczne do tego trójkąta jest wpisany w ten trójkąt, po odpowiednich wyliczeniach wyjdzie, że jest identyczny jak słoik

ad. 2 O którą średnicę ci chodzi? W każdym razie, w tym zadaniu są same figury foremne, więc można je powiekszać, zmniejszać a i tak będą do siebie proporcjonalne.
Duży garnek z 24cm do 2cm? no to słoiki będą miały średnicę 3/4 cm... itd.
Zresztą, mój rysunek jest w skali 1:2 :) moj garnek ma 12cm, sloiki po 4 a i tak wszystko ladnie sie wpisuje, i jakbym to pomnozyl przez 2 to i tak ladnie by sie wpisywalo... tylko by mi kartki braklo

U-boot [ Karl Dönitz ]

irenicus --> sprobuje raz jeszcze :)

pierwsze pytanie
napisales:

Budujemy trójkąt równoboczny na promieniach dużego okręgu, wipsujemy w ten trójkąt okrąg

jednak okrag jest wpisany wlasnie w pogrubiony trojkat, a nie w ten pierwotny stworzony z promieni

drugie pytanie:
uniwerslanosc, tzn zastosowanie tego sposobu do innych przypadkow, np: inna srednica sloikow, powiedzmy X - jakbys wtedy to rozwiazal ? tutaj skorzystales z trojkata rownobocznego (dlaczego ?)

mam nadzieje, ze jest moze troche jasniej

z gory dziekuje za poswiecony czas !

Pozdrawiam

p.s.
caly czas obracamy sie wokol rozwiazania graficznego,
rozumiem, ze analitycznie nie da sie tego ugryzc

irenicus [ Mareczek ]

Zacznę od końca :)
p.s - rozwiązanie przy którym posiłkujemy się rysunkiem to nie rozwiązanie graficzne :) rysunek tylko pomaga widzieć sytuację, reszte liczymy. jeżeli chciałbyś to w ogóle bez rysunku robić samym liczeniem... to musiałbyś to przenieść w układ współrzędnych czyli jeszcze więcej roboty... tylko po co?

No dobra, może kiedyś nauczę się jasno tłumaczyć...

Dobra, fakt, boki trójkąta leżą na promieniu ale wykraczają poza okrąg więc są dłuższe, po to zaznaczylem wysokość :) Znając wysokość i wiedząc, że to trójkąt równoboczny możesz łatwo policzyć jego boki, co też zrobiłem.

2. No to jeszcze raz... 24cm - garnek, 8cm - sloik -> stosunek średnicy garnka do sloika = 3
A zatem Xcm - garnek, X/3cm - słoik... rozwiązanie to samo tylko zamiast tych liczb bede mial X (czegoś tam)... Jeżeli garnek = Xcm, słoik = Y cm to jeżeli w treści zadania nie będą jakoś powiązane, to będzie to nie do rozwiązania... Będzie Co ma piernik do wiatraka :)

Tutaj skorzystales z trojkata rownobocznego (dlaczego ?)

Bo to taka moja metoda na wszelkie zadania z geometrii, jeżeli nie widzę metody rozwiązania odrazu, bazgram po rysunku (rysuję proste, styczne, wyznaczam kąty, uzależniam jedne niewiadome od drugich)

Ty tam na dole, tylko pamiętaj, że masz jeszcze udowodnić, że w środku mieści się 7 słoik...

U-boot [ Karl Dönitz ]

irenicus --> Oki,

Dziekuje !!

Pozdrawiam
milej nocy zycze !!

p.s. 1
spoko, Ty tam na gorze :-))

p.s.2
tak, na zakonczenie :)

w zadaniu pytamy (tak naprawde), nie o to ile wstawimy sloikow do garnka ale ile wstawimy trojkatow rownobocznych opisanych na tym sloiku o promieniu r=4
r=1/3h, zatem h = 12

h - pokrywa sie z promienim garnka, wiec wstawimy tam tylko 6 trojkatow (sloikow) o boku a
h= a 1/2 (3)^(1/2), wiec po przeksztalceniach a=8(3)^(1/2)

a siodmy sloik, 24-2x8=8, tyle zostaje srednicy w sroku, wiec sie zmiesci ;)

over & out

Glob3r [ Tots units fem força ]

[65]&[66]
A jednak źle myślałem. Aż wstyd pomylić się przy takim zadaniu na 10 dni przed maturą -.-
Dzięki :)

lajtowy ziomek:) [ God of War ]

Dział "Wielomiany".

Tak dla pewności, obliczanie sumy współczynników to np. W(1), zaś wyraz wolny, to W(0), tak?:)

jagged_alliahdnbedffds [ Rock'n'Roll ]

^
Co do sumy współczynników to się zgodzę, ale wyraz wolny to wg mnie wyraz wielomianu, przy którym nie ma 'x'. Np. w wielomianiu W = 3x^3 + 5x^2 - 4x + 7, wyrazem wolnym jest 7.


edit. No, dobra - to co napisałem jest równoznaczne z tym Twoim W(0), po prostu jakoś nigdy na to tak nie patrzyłem ;) Czyli masz całkowitą rację, panie lajtowy!

lajtowy ziomek:) [ God of War ]

@up----> Dzieki serdeczne za odp.:)

lajtowy ziomek:) [ God of War ]

Podniosę wątek, a nuż ktoś potrzebuje pomocy przy zadaniu przed zbliżającym się weekendem...

lajtowy ziomek:) [ God of War ]

Up.

lajtowy ziomek:) [ God of War ]

Nowy tydzień = nowe zadania do rozwiązania. :)
Śmiało, jak ktoś potrzebuje pomocy przy jakimś zadaniu, to proszę bez oporów je tutaj umieszczać, będziemy radzić...

lajtowy ziomek:) [ God of War ]

Coś słabiutko ostatnio z "życiem" tego wątku. Może jednak ktoś pomocy potrzebuje, śmiało, od tego jest ten wątek...

Powlol [ Spectrum ]

Ile wody trzeba dodać do 1 litra 6 procentowego octu, aby otrzymać ocet 5 procentowy??

Montera [ Michael Jackson zyje ]

1000g/x g wody = 5/1
5x = 1000
1000/5 = 200
x = 200

Odp: Żeby otrzymać ocet procentowy trzeba dodać...

Powlol [ Spectrum ]

Montera -> dzięki za odp ale możesz jeszcze bardziej to wyjaśnić? Bo po prostu nie rozumiem tego zadania....

Montera [ Michael Jackson zyje ]

1 l = 1000 ml

1000 ml - 6%
x ml - 5%

Zastosuj metodę "krzyżykową", czyli..

6/x x 1000/5 = 1200/x, wtedy wyjdzie, że ocet procentowy to 1200 ml. Później piszesz, że 1200 - 1000 = 200 ml.. tak też można zrobić :)

Powlol [ Spectrum ]

Montera - Wielkie dzięki

preDratronIX [ Generau ]

może mi ktoś pomóc?

Zadanie które napisze z pozoru może być łatwe, ale ja z tym do zajebania już jeden krok mam...

Mianowicie mam obliczyć długośc drutu na zbudowanie graniastosłupa praw. sześciokątnego o długości krawedzi podstawy 2cm i krawedzi H= 3cm.

Tak wiem, jest pewnie łatwe ale za cholere nie mogę zrobić.

Dodaję wszystkie krawędzie ale nic!@!!!22#@#

tomazzi [ Flash YD ]

12 krawędzi po 2cm i 6 krawędzi po 3cm.

preDratronIX [ Generau ]

tomazzi - dzięki.

A skąd tyle krawędzi? Tzn wiem, że krawędzie = 3n gdzie n to liczba kątów w graniastosłupie...

jagged_alliahdnbedffds [ Rock'n'Roll ]

^
A że sześciokąt ma, uwaga!, SZEŚĆ kątów, to 3*6 = 18 = 12+6, czyli tak jak napisał tomazzi.

preDratronIX [ Generau ]

[88]

Zdałem sobie sprawę z tego, że przez 3 mnoży się krawędzie z jednej ściany tzn. wszystkie krawędzie ze ściany podstawy i wszystkie krawędzie ze ściany bocznej

preDratronIX [ Generau ]

Może mi ktoś jeszcze pomóc z czymś takim?

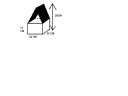
Zadanie polega na obliczeniu ilości puszek zużytych na zamalowanie zaznaczonych na czarno daszków.

Przyjmując że jedna puszka starczy na 10dm^2 materiału.

Nie wiem jak to obliczyć, czy w trójkącie (podstawie graniastosłupa trójkątnego) zastosować wysokość odejmując wysokośc graniastosłupa sześciokątnego od wysokości całkowitej (28 cm - 12 cm), a potem użyć twierdzenia pitagorasa.

Belert [ Legend ]

masz trojkat prostokatny o podstawie 12 cm i wysokosci 16 cm ,potrzebujesz przeciwprostokatnej.,wynosi 20.Pole jednej storny dachu to 30x20 =600 cm kw.
z tego co widac trzeba pomalowac 4 strony 2 zew. i 2 wew czyli 2400 cm kw.

preDratronIX [ Generau ]

w jaki sposób obliczyłeś przeciwprostokątną?

Chudy The Barbarian [ Legend ]

Z twierdzenia Pitagorasa.

Belert [ Legend ]

mysl ! jak nie ma podanych katow to masz tylko jedno wyjscie - tw.Pitagorasa :)

preDratronIX [ Generau ]

Wykonywałem twierdzenie pitagorasa! Ale nie wiem czy mi dobrze wyszło a mianowicie.


Aby obliczyć przeciwprostokątną trzeba było posłuzyć się wzorem

x2 = 16^2 + 12^2

x^2 = 256 + 144 = 400

... ups.. cholera...

Sory to moja wina. Źle policzyłem. Używałem Pitagorasa w ten sposób ale źle mi wyszło. Przepraszam jeszcze raz.

preDratronIX [ Generau ]

Ostatnia prośba i nikogo nie męcze.

Zadanie jest z gwiazdką

*10 "Różnica długości dłuższej i krótszej przekątnej graniastosłupa prawidłowego sześciokątnego o równych wszystkich krawędziach wynosi 10cm. Jaka jest długośc krawędzi tego graniastosłupa?"

Za cholerę nie mogę zrobić :<.

jagged_alliahdnbedffds [ Rock'n'Roll ]

^
Narysuj wszystko i pozaznaczaj. Jeśli "a" i "b" to odpowiednio dłuższa i krótsza przekątna graniastosłupa, a "c" - krawędź podstawy = krawedź boczna = krawędź graniastosłupa, to rysujesz dwa trójkąty i z twierdzenia Pitagorasa obliczasz długości "a" i "b". Będą one uzależnione od "c", ale wiesz również, że a = b + 10, więc wyliczasz "c" i koniec zadania. W spoilerze obliczyłem na szybko, więc mogą być błędy obliczeniowe.

preDratronIX [ Generau ]

[97] To dziwne

w odpowiedz pisze że 10(<pierwiastek z 5> + 2) = (w przybliżeniu) 42,4 cm

czyli + a nie minus.

preDratronIX [ Generau ]

Własnie zdałem sobie sprawę z tego że nie kumam Twojej wypowiedzi.

Napisałeś że a= B+10.

niech będzie b=2a
a a= a/v3

jagged_alliahdnbedffds [ Rock'n'Roll ]

Napisałem na początku jakie są założenia, czyli co znaczy każda literka.

Napisałeś że a= B+10.

Różnica długości dłuższej i krótszej przekątnej graniastosłupa wynosi 10 cm, więc dłuższa przekątna = krótsza + 10 cm, co przechodząc na literki wygląda tak: a = b + 10.

Dalszej Twojej wypowiedzi z kolei ja nie rozumiem, więc napiszę moje rozwiązanie:

a = c*pierw(5), b = 2c, a = b + 10
c*pierw(5) = 2c + 10
-10 = 2c - c*pierw(5)
-10 = c*(2 - pierw(5))
c = -10/(2-pierw(5)) = 10/(pierw(5)-2) =około= 42,4 cm

Czyli odpowiedź mam dobrą. Widocznie to to samo :)


edit. To jest to samo, bo Twoja odpowiedź równa się mojej po usunięciu niewymierności z mianownika.
Banalne to zadanie z gwiazdką, a w liceum nie potrafiłem takich rozwiązywać - jednak studia czegoś uczą ;D

preDratronIX [ Generau ]

a czy a nie powinno się równać

a= c*pierw(3)??

bo u Ciebie jest napisane, iż 5

preDratronIX [ Generau ]

Kurwa! (przepraszam ale już mnie coś ponosi)

Skąd jest pierwiastek z pięciu????

Edit: pierwiastek z pięciu pochodzi od wzoru na dłuższą przekątną graniast. od krawędzi...?? My nawet do cholery tego nie mieliśmy!

preDratronIX [ Generau ]

Jeszcze jedna rzecz, dzisiaj na lekcji robiliśmy zadanie o treści

"Pole powierzchni graniastosłupa prawidłowego 6 kątnego jest równe 240 pierw.(3), a krawędź podstawy wynosi 8 cm. Oblicz dł. przekątnej ściany bocznej."

Narazie napisałem

Pc= 240 pierw z 3 cm^2
Pp= 6x a^2 pierw z 3:4
Pp= 6x 64(8^2) pierw z 3 :4
Pp = 96^3 cm2
Pb= Pc-2Pp
Pb= 240 pierw. z 3 - 192 pierw z 3
Pb= 48 pierw. z 3 cm^2
Pś= 48 pierw. z 3 : 6= 8 pierw z 3 cm^2

I dalej nie wiem. Jak obliczyć przekątną Ściany bocznej?

Montera [ Michael Jackson zyje ]

Przekątna ściany bocznej to po prostu przekątna boku.

preDratronIX [ Generau ]

Graniastosłup prawidłowy sześciokątny. Sory.

Zresztą jest napisane

jagged_alliahdnbedffds [ Rock'n'Roll ]

Skąd jest pierwiastek z pięciu????

Z Pitagorasa --> a^2 = c^2 + 4*c^2 --> a = c*pierw(5)

Tego się nie bierze w szkole tylko wystarczy narysować te trójkąty, o których mówiłem Ci w pierwszym poście dotyczącym tego zadania!


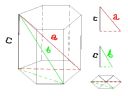
edit. Idź i nie grzesz więcej! -->
+ gdzie masz napisane jakie długości ma dłuższa i krótsza (na rys. czerwona i zielona linia przerywana) przekątna sześciokąta foremnego.

jagged_alliahdnbedffds [ Rock'n'Roll ]

[103]
P - pole powierzchni
a - krawędź podstawy
b - krawędź boczna
c - szukana przekątna ściany bocznej

P = 2*Pp + Pb
Pp = 3*a^2*pierw(3)/2
Pb = 6*a*b
P = 3*a^2*pierw(3) + 6*a*b

c^2 = a^2 + b^2

Mając dane "a" i "P" obliczasz "b", a następnie "c" z Pitagorasa :)

preDratronIX [ Generau ]

[107] To jest sześciokąt więc skąd 3???

Poza tym wynik wychodzi pierwiastek z 91 (przekątna ściany bocznej...)

Namieszałeś już mi :<

I tam się dzieli przez cztery a nie dwa >>:O

jagged_alliahdnbedffds [ Rock'n'Roll ]

Wzory wziąłem z Neta, więc są na pewno dobrze.

Błąd w obliczeniach zrobiłem:

P = 3*a^2*pierw(3) + 6*a*b, c^2 = a^2 + b^2
240*pierw(3) = 3*8^2*pierw(3) + 6*8*b
5*pierw(3) = 4*pierw(3) + b
b = pierw(3)
c^2 = 64 + 3
c = pierw(67)

Jeśli wychodzi inaczej, to znaczy, że masz błąd w książe ;)

lajtowy ziomek:) [ God of War ]

Nowa część: https://forumarchiwum.gry-online.pl/S043archiwum.asp?ID=10297909&N=1