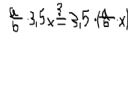--> Archiwum Forum
--> Archiwum Forum
Jak się oblicza metry kwadratowe? :)
reksio [ Q u e e r ]
Jak się oblicza metry kwadratowe? :)
Matematykę skończyłem już dawno i głupim z tego, że hej.
Załóżmy więc, iż coś ma 1023 metry długości i 150 metrów szerokości (prostokąt). Ile to metrów kwadratowych? Chodzi mi o wzór...
Dzięki za pomoc.
alpha_omega [ Senator ]
1023*150
Wyobraź to zresztą sobie. Metr kwadratowy to kwadrat o bokach długości metra. Teraz masz pionową linię długości 1023 metrów, jeśli od tej linii rozciągniesz płaszczyznę na szerokość 150 metrów, to łatwo zauważyć, że każdy jeden z 1023 metrów zamienia się w 150 metrów kwadratowych :)
Na pewno nie jest to prowokacja? ;)
reksio [ Q u e e r ]
LOL. Dzięki alpho :)
beowulff [ X ]
axb
153450 m2
Macco™ [ CFC ]
oł gad xD
to jest podstawa uczyli tego w 4 klasie podstawówki
reksio [ Q u e e r ]
alpho-> Naprawdę nie jest :)
Macco-> Musiałem opuścić tę lekcję :>
reksio [ Q u e e r ]
To teraz sam spróbuję-
rozumiem, iż 41886 metrów kwadratowych to 418860000 centymetrów kwadratowych? :)
Ogon. [ Uzależniony od Marysi ]
tak :)
reksio [ Q u e e r ]
Widzicie, szybko się uczę xD
A na serio - nawet filologom przydałaby się matma... bo tak patrząc na moje umiejętności, to się aż smutno robi. :>
stanson [ Szeryf ]
e tam smutno, ja się ubawiłem :P
beowulff [ X ]
Wiesz co, tak mnie zaskoczyles ze zanim napisalem posta sprawdzilem w tablicach czy to napewno to XD
alpha_omega [ Senator ]
reksio -------------> Dlatego ja proste zadanka matematyczne dla własnej przyjemności rozwiązuje, a właściwie to mam zamiar - ale zabieram się do tego już od dawna, więc może to taki zamiar dla zamiaru - dokształcić się dużo ponad program licealny; ot chociażby po to, ażeby rozkminić o co dokładnie chodzi w teorii względności.
beowulff ----------> Serio? To może ja dlatego mam jakieś zahamowania matematyczne i choć niby rozumiem coś, to nie rozumiem (nie czuję?), choć na 10 sposobów sobie tłumaczę, dalej nie jestem przekonany. Może to po prostu chorobliwa niepewność?
BarD [ Leningrad Cowboy ]
W sumie ta matematyka obowiązkowa na maturze nie taki głupi pomysł :-)
reksio [ Q u e e r ]
alpha-> Ja zawsze wolałem jednak Mickiewicza niż teorię względności. Ew. teorię sublimacji :)
Krasper [ Konsul ]
reksio---> Nawet Mickiewicz studia zaczynał od nauk ścisłych : ). Dopiero później sie przerzucił. Nie śmieję się bo też nienawidzę wszelkiego liczenia.
BIGos [ bigos?! ale głupie ]
reksiu, nie kalecz ;)
reksio [ Q u e e r ]
Krasper-> Ja zaczynałem od zapałek. Oceny z matmy miałem dobre do czasów liceum. Potem nauczyciel, koledzy i przede wszystkim zamiłowanie do humanizmu zupełnie oddaliły mnie od tej dziedziny. Jedynie z chemii utrzymałem dobry. Reszta dopy :)
alpha_omega [ Senator ]
Ale matematyka jest naprawdę interesująca, wręcz fascynująca. Trzeba się tylko wyzbyć zahamowań. Jak widzicie ja się jeszcze ostatecznie ich nie wyzbyłem - bo jak nazwać to, że mając przetłumaczone sobie na dziesiątki sposobów to, dlaczego mnożenie jest przemienne (a to przecież szkolna oczywistość), łapię się na tym, że znowu się zastanawiam. Czasami mi się wydaje, że bez mechanizacji tzn. rozwiązywania setek zadań, co powoduje wejście pewnych form niemal w podświadomość, matematyki się nie da tak naprawdę nauczyć, a nierozwiązywanie zadań powoduje matematyczne ociemnienie i podważanie zdrowego rozsądku nawet rachunkowego.
Też tak miałem - w podstawówce byłem z matematyki jednym z lepszych uczniów, w pierwszej LO jeszcze coś tam uważałem, a później odpływ od przedmiotów ścisłych i teraz wręcz wydaje mi się czasami, że mam jakieś upośledzenie matematyczne. Być może olewanie w pewnym wieku pewnych rzeczy uniemożliwia ich nadrobienie, nie wchodzi to po prostu później w podświadomość. Sam nie wiem - być może to raczej jakieś zahamowanie, strach, zatracone wyczucie odpowiedniego podejścia.
beowulff [ X ]
alpha_omega -> metry kwadratowe mam na codzien, w projektach budowlanych, ale takiego szoka dostalem ze nie bylem pewny czy to to :)
Taka anegdota, bylem w klasie Mat-Fiz-In i na probnej maturze z matmy bylo 30 jedynak na 30 osob, a zadania byly tak proste ze robienie ich zajmowalo pare min, ale wszycy myslelismy ze trzeba cos wiecej zrobic i efekt byl taki ze nikt nic poprawnie nie napisal
Macco™ [ CFC ]
alpha --> też interesuję się matematyką i sam czasami łapię się na tym że sprawdzam czy mogę coś pomnożyć na odwrót(zgodnie z zasadą) ale to tylko przy trudniejszych i bardziej rozbudowanych zadaniach
alpha_omega [ Senator ]
beowulff --------------> No to ja mam coś podobnego cały czas, a właściwie znacznie gorzej. Wiem np. jak rozwiązać zadanie, ale jakoś nie mogę przyjąć rozwiązania, które sprytnie wiąże jakieś odpowiednie fakty, lecz chcę to widzieć jakby naocznie, do dna, w całym mechaniźmie. Można chyba powiedzieć, że mój mózg odrzuca abstrakcję, bazowanie na wybranych faktach.
Przykładowo mam takie rozkminki:
Dlaczego a b-tych jest równie, a:b tzn. dlaczego a dzielone przez b, jest równe ułamkowi z jedności wynoszącemu a/b, gdzie a<b i a,bEN.
Dzielenie a przez b możemy sobie wyobrażać jako podzielenie a na b równych części ('a' traktujemy jako zbiór jedności o mocy a, który mamy przekształcić w zbiór o mocy b zachowując tę samą wartość sumy elementów). Mamy dwa zbiory: zbiór o mocy a (złożony z jedności), i zbiór o mocy b-a (którego elementy to na razie zera). Z każdego elementu zbioru 'a' (z każdej jedności) musimy się pozbyć b-a pewnych równych sobie wielkości takich, ażeby po rodzieleniu ich na b-a, elementy zbioru 'a' były równe elementom zbioru b-a. Ostatecznie na każdy element zbioru o mocy b-a przypada 'a' takich wielkości. Jednocześnie jest to wartość równa tej, jaką ma teraz każdy element zbioru 'a', który jest teraz mniejszy od wyjściowej jedności o b-a. A więc uzyskana wartość to a/a+(b-a)=a/b wyjściowej jedności.
alpha_omega [ Senator ]
Dokładniej:
Dlaczego a b-tych jest równie, a:b tzn. dlaczego a dzielone przez b, jest równe ułamkowi z jedności wynoszącemu a/b, gdzie a<b i a,bEN.
Dzielenie a przez b możemy sobie wyobrażać jako podzielenie a na b równych części ('a' traktujemy jako zbiór jedności o mocy a, który mamy przekształcić w zbiór o mocy b zachowując tę samą wartość sumy elementów i ich równość).
Mamy dwa zbiory: zbiór o mocy a (złożony z jedności), i zbiór o mocy b-a (którego elementy to na razie zera). Z każdego elementu zbioru 'a' (z każdej jedności) musimy się pozbyć b-a pewnych równych sobie wielkości x takich, ażeby po rodzieleniu ich na b-a, elementy zbioru 'a' były równe elementom zbioru b-a. Ostatecznie na każdy element zbioru o mocy b-a przypada 'a' takich wielkości x. Jednocześnie jest to wartość równa tej, jaką ma teraz każdy element zbioru 'a', który jest już mniejszy od wyjściowej jedności o (b-a)x. A więc uzyskana wartość to ax/ax+(b-a)x=ax/bx=a/b wyjściowej jedności.
kiowas [ Legend ]
alpha ---> jeśli zajmujesz się taką magią z czystej ciekawości to podziwiam....i nie rozumiem :))
BIGos [ bigos?! ale głupie ]
alpha - za duzo kombinujesz
a:b = a/b
nie musisz miec na to zadnego dowodu, to jest po postu to samo. Takie samo "to samo" jak przy czajnikach, krzesłach itd. Ta sama wartość, po prostu różny sposób zapisu. Tego sie nie dowodzi. Jedyna droga do głębszego zbadania tego, to liczenie na palcach. Dowody pochodzą z realnego życia, to aksjomaty.
EG2006_43991898 [ Nadworny krasnal ]
kiowas>>> ja dla samej przyjemności liczenia robie zadania do przodu :D
Y0D4 [ Pretorianin ]
Każdy tuman, który nie umie dodawać, twierdzi, że jest humanistą.
Cytat zaczerpnięty z pewnej pierdółki :)
alpha_omega [ Senator ]
BIGos -------------->
Nieprawda, to nie jest dokładnie to samo tzn. są to zapisy równoważne, ale to, że dla Ciebie nie wymaga to dowodu, wynika tylko i wyłącznie z tego, że tak Ci wpojono w szkole - to samo i basta. Jestem zupełnie pewien, że u zarania matematyki dla kogoś to był problem, bo nie jest jasne jak to, że widze przed sobą monitor, iż mając 6 tortów i dzieląc te 6 tortów na 7 osób, zostanie każdej osobie dokładnie 6 kawałków z tortu podzielonego na równe 7. Równoważność zachodzi zawsze, ale myślenie tych dwóch zapisów jako identycznych, to wynik szkolnej edukacji.
I właśnie to jest jedno z moich podejrzeń - matematyki się uczy w olbrzymiej mierze tak, że rozwiązując setki zadań, pewne formy myślenia doprowadza się do stopnia podświadomego niemal mechanizmu, następuje mechanizacja rozumowania. I kto wie, czy nie czasem to (kiedy poziom umysłowy ogólnie jest równy) dzieli osoby mające z matematyką problemy, od tych, które tych problemów nie mają.
BIGos [ bigos?! ale głupie ]
alpha - nie rob ze mnie debila
Ten czy inny zapis oznacza dokładnie jedną wartość liczbową i tylko JĄ reprezentuje. Możesz to rozkminiać do woli, ale tu nie ma niczego więcej do rozumienia. Niemal każdą wartość możesz zapisać na nieskończoną ilość sposobów.
A te torty mógłbyś przedstawić nawet jako posiekane, gdyż z punktu widzenia matematyki te ilości się nie różnią.
Nigdy nie robiłem zadań matematycznych w domu (teraz zaczynam studia, więc pewnie zacznę) więc nie zwalaj tego na mechanizacje.
alpha_omega [ Senator ]
BIGos ---------------->
Nie robię z Ciebie debila, taka jest prawda, a że to zawsze jest równoważne sam napisałem (pytanie: dlaczego jest równoważne?). Nie musisz niczego liczyć na palcach. Pokażę Ci to na tortach (przykład konkretny, ale przy wyćwiczeniu w abstrakcji można to myśleć bez konkretów, samymi pojęciami).
Masz 6 tortów i siedem osób. Co musisz zrobić, ażeby rozdzielić to równo? 6 osób musi oddać po równym kawałku tortu takim, ażeby następnie wszyscy mieli po równo. A więc 7 osoba uzykuje 6 takich kawałków, każda inna ma 6, a że oddała po jednym, więc ma 6/7 wielkości wyjściowej.
Nawet nie wiesz jakich rzeczy się dowodzi - istnieje kilkusetstronicowy dowód dodawania dwóch liczb naturalnych wyprowadzony z zasad logicznych (Russell'a bodajże). Tak - są to wielkości równoważne; nie - ich myślenie nie jest w sposób naturalny identyczne, bo żeby dojść do tego, że są równoważne, najpierw myśleć trzeba je w sposób rózny i znaleźć wspólny mianownik myśli. Nie są równoważne chociażby z tego powodu, ze inaczej się myśli dzielenie 6 tortów na 7 osób, a inaczej jednego na siedem części i branie z tego 6. Zresztą ten swego rodzaju dowód jaki podałem można z całą pewnością uściślić do czystej matematyki i będziesz miał dowód. Jakieś aksomaty przyjąć na początku trzeba, ale ta równoważność daje się dowodzić na podstawie właśnie takich możliwie najprostszych aksjomatów, sama aksjomatem być nie musi.
BIGos [ bigos?! ale głupie ]
to co opisałeś to jest właśnie dowodzenie 'na palcach'
a co do kilusetstronnicowych dowodów - jeśli czytałeś jakieś teksty matematyczne, to dobrze wiesz, w jak skomplikowany sposób można zapisywać proste rzeczy.
wiesz, mi sie wydaje że masz problem raczej natury teologicznej - chcesz uwierzyć w matematykę. A ją trzeba rozumieć. Jeśli przeczytałeś dowód i go zrozumiałeś, a do tego nie potrafisz wskazać błędów - możesz przyjąć że dowód jest prawdziwy. I nie ma miejsca na wątpliwości.
Macco™ [ CFC ]
zgodzę się z Bigosem bo to tak jakbyś się zastanawiał dlaczego a*b i ab to to samoa przecież to oczywiste
alpha_omega [ Senator ]
BIGos ---------------> Co Ty pleciesz. Sorry za wyrażenie, ale sam się prosisz. Kto tu chce wierzyć w matematykę? Właśnie Ty chcesz w nią wierzyć, a nie rozumieć; ja natomiast odwrotnie. To ja tę równoważność tłumaczę, a nie przyjmuję jako prawdę objawioną; to Ty twierdzisz, że należy to przyjąć, a nie tłumaczyć. Więc coś chyba nie hallo z Twoim zarzutem.
Natomiast zgadzam się co do jednego. Mogę przeczytać dowód, nie znaleźć w nim błędów i go zrozumieć, a jednak następnie kiedy z tego mam skorzystać znów nachodzą mnie wątpliwości, bo chciałbym to za każdym razem odczuwać tak, jak w momencie owego zrozumienia, z tym błyskiem łączenia się wszystkiego, tą chwilą iluminacji. I być może to jest dość chorobliwe, ale wynika właśnie z niewiary, chęci ciąłego głębokiego rozumienia, wynika właśnie z niemożności przyjęcia czegoś (nawet wcześniej zrozumianego) i mechanicznego wykorzystywania.
Macco™ -------------> Nie - to ani trochę nie jest tak. W Twoim przykładzie jest to różnica zapisu. W moim w żadnym wypadku, bo mieć np. 6 całości i podzielić to na siedem części, a mieć jedną całość, podzielić to na siedem części i wziąć sześć, to nie jest w żadnym razie różnica jedynie zapisu. Dojdziesz do takiego samego wyniku, ale myśląc od zupełnie innej strony i właśnie równoważność tych dwóch form myśli trzeba wykazać. Lepiej byłoby, gdybyś napisał a*b, a b*a - tu też nie jest to jedynie różnica zapisu, kryje się w tym zagadka.
BIGos [ bigos?! ale głupie ]
W moim poście chodziło właśnie o to, co napisałeś w swoim drugim akapicie. Niezręcznie to ująłem.
Bardzo dziwnie masz, bo np. kiedy mnie nachodza podobne wątpliwości - po prostu przypominam sobie o co chodziło w dowodzie. Oczywiście nie cały, długaśny wywód, z zastrzeżeniami, kwantyfikatorami itp. nudną, ale potrzebną pisaniną tylko samą esencje. "To jest tak, więc to jest równe temu i z tego wynika takie coś". Nie wiem w jaki sposób znając dowód możesz mieć jakies wątpliwości, chyba mnie to przerasta ;)
alpha_omega [ Senator ]
BIGos --------------->
Bo dowód to ciąg myśli, takie sztywne rozumowanie. To jest tak, a więc to jest tak, wniosek, że musi być tak. To jest rozbite w czasie, suche, takie typowo logiczne wiązanie kolejnych ogniw, gdzie przy ostatnim nie pamiętasz już pierwszego, albo nawet poprzedniego, jest tylko suchy wniosek.
Ale przecież - musiałeś tego doświadczyć - jest taki moment zrozumienia (nie zawsze się pojawia), że przez chwilę coś wydaje się kompletnie oczywiste, jak prawda objawiona, tak jakby widzisz na raz wiele zależności, wiele obrazów (nie zawsze są to obrazy), jakby wszystko spaja jedno uczucie, całość zlewa się w przebłysk oczywistości, wręcz szokuje, uderza jasnością, to właśnie nazwano Eureka.
I ja mam jakoś tak, że mi się to od kilku lat rzadko pojawia, a przede wszystkim nie potrafię sobie powtórzyć rozumowania tak, ażeby znowu to uczucie wydobyć, ażeby doprowadzić do takiej jasności, tego przeżycia niemal estetycznego. Przy tym wszystkim ja chę, muszę, wydaje mi się, że tak być powinno, rozumować z ciągłym takim odczuciem.
Wydaje mi się, że jak korzystam z przemienności mnożenia to powinienem w tym momencie widzieć z taką właśnie janością tą przemienność (bo daje się ją rozjaśniać np. tym, że skoro 'b' mamy 'a' razy, to każda jedność 'b' występuje 'a' razy, a więc 'a' mamy 'b' razy; ale to powinna być myśl punktowa, swego rodzaju oświecenie, taka głębia wejrzenia kiedy widzi się na raz całą pełnię); jak korzystam z jakiegoś prawa, chę widzieć z tą jasnością wszelkie zależności w tym prawie, jak wcześniej, w tym momencie pierwszego najczęściej zrozumienia. Wydaje mi się, że tak być powinno, bo to - tak mi się wtedy zdaje - dopiero jest rozumienie, a ponieważ to się nie dzieje, rozkminiam rzecz od początku mając nadzieję, że się pojawi.
No i stąd moje zachowania.
Macco™ [ CFC ]
alpha ---> IMO ty tłumaczysz sobie to łopatologicznie co dla mnie wydaje się oczywiste
alpha_omega [ Senator ]
Macco™ ------------> Ale dla Ciebie to wydaje się oczywiste, tak jak jeszcze parę lat temu dla mnie. Bo nie rozkminiasz tej oczywistości. Sam się często łapię na tym, że jak np. pomagam rozrysowywać drzewka spadkowe, a ktoś popełnił gdzieś błąd, to automatycznie niemal wszystko skrótowo (niektórzy chcą po kolei liczyć wszelkie ułamki tylko dlatego, że suma wyjściowa się zmieniła, a wiadomo, że stosaunki pozostają te same) liczę, mnożę, dzielę, korzystam z przeminności mnożenia i nawet tego nie zauważając, że z niej korzystam podaję oczywisty dla mnie wynik. Ale nie jest to ta oczywistość - taka oczywistość to bardziej mechanizacja, podświadomość procesów myślowych, a nie owo wejrzenie w istotę.
Macco™ [ CFC ]
może za parę lat też będzie mnie to zastanawiać więc ciesze się obecnym błogim stanem mego umysłu ;)
taka oczywistość to bardziej mechanizacja, podświadomość procesów myślowych, a nie owo wejrzenie w istotę
zwał jak zwał uznajmy że to miałem na myśli :P hehe
alpha_omega [ Senator ]
PS. Wytłumacz mi np. dlaczego ułamek a/b z liczby 3,5 raza większej, niż x, jest 3,5 raza większy, niż ten sam ułamek z x. Tylko proszę bez takich, że - stosując przeminność mnożenia... etc.
BIGos [ bigos?! ale głupie ]
alpha - dla mnie zrozumiany dowód jest jakby całościową strukturą zagadnienia... jedno wynika z drugiego, wiąże się z trzecim i w naturalny sposób daje wniosek.
Hmm, mi sie to uczucie objawienia, o którym piszesz, pojawia jak tylko podchwycę jakąś nową ideę, jak zrozumiem coś, o czym wcześniej nie miałem pojęcia. I - może nie mówimy o tym samym - to uczucie mi zostaje. Stosując udowodnione metody lubie ogarniać jak najszerszy obraz zadania - np. doskonale zdaje sobie sprawe z zależności między wartościami (nie wszystkich, to pewne, ale tych które znam i o których pamiętam). Naprawdę wydaje mi się, że nie tylko ja tak mam, ale raczej większość ludzi. Wydaje mi się, że to właśnie nazywamy rozumieniem matematyki.
Praktyka pozwala na dostrzeganie o wiele większej ilości zależności, ale w mniejszym lub większym stopniu każdy na poziomie LO musi je dostrzegać.
Owszem, można walić pamięciówę, typu - "jeśli iks jest pod kreską to musze napisać że nierówne zero, potem xxx a potem zzz" - ale ten typ rozumowania kopńczy się na gimnazjum. To jest ta twoja mechanizacja rozumowania. To dobrze, że się nią nie posługujesz, bo to nie jest matematyka tylko tresowanie.
edit: widze ze napisalismy to samo ;)
Macco™ [ CFC ]
jeśli cię dobrze rozumiem to chcesz żebym ci udowodnił to ---->
a dla mnie to jest rzecz oczywista jak za przeproszeniem kupa u 2 miesięcznego dziecka !
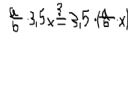
alpha_omega [ Senator ]
BIGos ----------->
No to mamy dwie możliwości: albo mi coś się stało z mózgiem, co od dłuższego czasu podejrzewam i co jest najbardziej irytującą mnie rzeczą od długiego czasu, i po prostu te chwile objawień mi się nie kodują i w ogóle jakoś moje myślenie stało się płaskie, bez głębi, bez uczuć (otępienie?); albo mówimy o czymś innym.
Piszesz:
Stosując udowodnione metody lubie ogarniać jak najszerszy obraz zadania - np. doskonale zdaje sobie sprawe z zależności między wartościami (nie wszystkich, to pewne, ale tych które znam i o których pamiętam).
Widzisz - znasz i pamiętasz i je dostrzegasz. Ja natomiast od razu bym myślał w ten sposób - mamy tu takie zależności oparte o to i o to (a i b), ale zaraz... to a i b przecież też wynika z jakichś zależności, dlaczego ja od razu nie widzę tamtych zależności, na czym te zależności polegały (tu mogę sobie powtórzyć dowód zależności a i b sto razy, ale wciąż szukam tego uczucia iluminacji, widzenia w głąb tych zależności, a nie jedynie przekonania, że są one prawdziwe - zresztą tego przekonania poprzez to, że nie mogę nagle spojrzeć w głąb, jakby objąć jednym spojrzeniem całego ich dowodu, też nie mam), bo przecież nie mogę się nimy ot tak po prostu posłużyć, choć znam ich dowód; bo to nie jest rozumienie etc. etc.
Macco™ -------------> Ale mnie nie obchodzi, że to jest dla Ciebie oczywiste, ja też w pewien sposób mogę to uznać, za oczywiste dla mnie. Chcę, ażebyś mi to rozjaśnił, wytłumaczył bez posługiwania się stwierdzeniami typu: korzystając z przemienności mnożenia; zobrazował w pewien sposób, pokazał mechanikę tej równoważności.
BIGos [ bigos?! ale głupie ]
Macco - chyba i tak nie rozumiesz o co chodzi alphie.
To milo, ze takie rownanie jest dla ciebie oczywiste, dla niego tez. Mozna to nawet pokazac na klockach lego. Nie w tym rzecz. Chodzi o to, zeby cos takiego udowodnic za pomoca instrumentow logicznych i matematycznych.
alpha - jesli dlugo nie miales stycznosci z matematyka to moze brak wycwiczenia? praktyke w rozwiazywaniu coraz trudniejszych zadan nabywa sie bez mala w dziesiatki lat, a stracic mozna w rok zmywania garow po 8 godzin dziennie.
alpha_omega [ Senator ]
Nawet niekoniecznie logicznych i matematycznych, chodzi m.in. o to, ażeby wydobyć z tej jasności, to na czym się ona opiera i nie przekonać się przypadkiem, że opiera się na wmówionym mechaniźmie, który nie angażuje żadnej myśli (np. jest neuronalne powiązanie - to jest w stosunku do tego tak, a nie inaczej i jest tak przy wszelkich podobnych formach logicznych; bez żadnego rozumienia, czy widzenia).
A z matmą nie miałem do czynienia przez kilka dobrych lat.
gkowal [ Centurion ]
alpha_omega jest klasycznym przykladem dlaczego humanisci nie powinni zajmowac sie naukami scislymi.
Przynajmniej na powaznie.
alpha_omega [ Senator ]
Np. w tym wypadku janość może wcale nie opiera się na widzeniu, że mnożąc x przez 3,5 mnożymy przez 3,5 każdą jego część, a więc a/b jest mnożone 3,5 raza i |a-b|/b jest mnożone 3,5 raza, a zatem ostatecznie obie te wielkości pozostają w takim samym stosunku, a 3,5*(a/b*x)stanowi a/b*(3,5x). Może nawet samo skrócenieułamka wcale nie jest wynikiem rozumienia (zważywszy na to co mówią wykładowcy uczelni wyższych i na matematykę kierują się ludzie bez rozumienia ułamków), bo może nie jest wcale oczywiste, że czym jest sam stosunek, lub ułamek. Kto wie co się kryje za tym błyskawicznym przejściem do uznania równoważności?
gkowa ------------> Proszę, towarzyszu, wytłumaczcie mi mechanikę wzoru:
Sn=(a1*(q^n-1))/q-1
dlaczego taka właśnie zależność miałaby nam dawać sumę wyrazów ciągu geometrycznego. Jak to rozumiecie, jak wyprowadzacie.
alpha_omega [ Senator ]
gkowal ---------------> Czekam :) No w końcu chyba nie jesteście humanistą.
gkowal [ Centurion ]
nie za bardzo wiem o co Ci chodzi z mechanika wzoru, ale zapewne chcesz mi tu pokazac ze przemnozyles rownanie przez 1 czyli (-1)/(-1), tak?
edit: bo klasyczne ujecie tego wzoru jest jednak nieco inne Sn=a1*(1-q^n)/(1-q)
A sam wzor sumy n wyrazow ciagu jest wyprowadzany (przynajmniej powinien byc) na lekcjach matematyki w kazdej klasie mat-fiz liceum
alpha_omega [ Senator ]
Nie - chodzi mi o to, dlaczego taka właśnie zależność (masz tutaj i mnożenie i potęgę i dzielenie i odejmowanie) daje sumę wyrazów ciągu.
Arcy Hp [ Legend ]
A ja własnie rozpoczynam od poniedziałku studia na AGH wydział Majcy Stosowanej. Nie ma to jak miły akcent matematyczny przed początkiem studiów :)
BIGos [ bigos?! ale głupie ]
Arcy HP - informatyka z Wrocławia się do ciebie uśmiecha ;)
alpha_omega [ Senator ]
gkowal -----------> I cóż z tego, że jest wyprowadzany. Mi chodzi o rozumienie tego wzoru nie poprzez wyprowadzenie (które jest rachunkiem), ale poprzez jego swoistą mechanikę. Patrzysz na wzór i mówisz - tak, a tak to działa i dlatego daje sumę wyrazów ciągu. Wyprowadzenia... heh, specjalnie pytam, żeby zsondować - jest rozumienie, czy go nie ma. Zarzuciłeś mi, że jestem humanistą nie nadającym się do ścisłego rozumowania. Popytaj kolegów ścisłowców - jaka jest mechanika tego wzoru, jakie określenie pewnego mechanizmu, używane również w programowaniu, tutaj pasuje.
Popytaj ścisłowców licealistów. Zobaczymy ilu będzie wiedziało.
Arcy Hp [ Legend ]
A informatyke też będe tam miał, póki co na I-szym roku mam IT. Potem przez 4 lata informatyke, ciekawe na jakim będzie ona poziomie...
gkowal [ Centurion ]
alpha_omega --> lol, i wlasnie dlatego humanisci powinni trzymac sie z daleko od nauk scislych.
Dla matematyka wyprowadzenie wzoru jest zarazem wyjasnieniem jak i dlaczego tak to dziala.
Niektore zlozone zagadnienia miewaja swoje bardzo proste finalne wzory i bardzo trudno jednym rzutem oka na wynik ostateczny okreslic skad sie to bierze.
alpha_omega [ Senator ]
Rekurencja. Wzór podałem specjalnie w wersji nieklasycznej - o ile jestem w stanie sądzić jako nienadający się humanista, nie robi to róznicy i o ile jestem w stanie sądzić jako humanista właśnie, ta wersja lepiej się nadaje do zobrazowania problemu.
-(a1/q-1) odrzucamy, bo to możemy sobie odjąć później
Mamy:
(a1q^n)/q-1
gdybyśmy dzielili to przez q, mielibyśmy oczywiście a1q^(n-1). Ponieważ jednak zostaje nam jeszcze 1*a1q^(n-1), musimy dodać jeszcze tę wielkość dzieloną przez q-1. A więc ostatecznie mamy:
a1q^(n-1)+(a1q^(n-1))/q-1
Odnośnie (a1q^(n-1))/q-1 powyższe rozumowanie powtarzamy. Itd. Itd. Itd. aż będziemy mieli - po odjęciu jeszcze odłożonej części - pełną sumę. Mówisz, że trudno pewne rzeczy określić - ja rozumiem (pomijając to, że taki Ulam jednym rzutem oka podał z dużą dokładnością wynik działania, które później - w trakcie prac - najtęższe głowy ówczesnego świata rachowały przez kilkadziesiąt minut). Ale rekurencja - o ile się orientuję poprzez kolegę z matematyki - jest wykładana na studiach i jest wykładana dlatego, że jest formą myśli obok tego, że bardzo wysublimowaną i często trudną do ujęcia, występującą w wielu zagadnieniach i potrzebną w rozumowaniach matematycznych.
Pichtowy [ Generaďż˝ ]
alpha_omega -> polecam Ci książkę Szczepan Jeleński "Lilawati" albo Martin Gardner "Moje najlepsze zagadki matematyczne i logiczne" sporo fajnych zadań matematycznych które rozruszają CI mózgownicę. BO z mózg jest jak mięsień- nie trenowany zanika, może nie bezpośrednio ale jego zdolności logicznego myślenia i rozwiązywania problemów/zagadek.
alpha_omega [ Senator ]
Pichtowy ------------->
Dzięki, choć wydaje mi się, że u mnie problem jest poważniejszy, niż jedynie brak praktyki.
Jak czytam np. dowcip: co wpisuje do rubryki 'zawód' Kaczyński? Kaczmarek; i przez chwilę siedzę nie wiedząc o co chodzi, albo jak czytam dowcip: Podchodzą policjańci do pijanego jegomościa na mieście. Jeden z nich z nutą kpiny wydaje polecenie: - Zapraszamy do poloneza. Jegomość na to "Dddzziękkkuję, z sukami nie tańczę"; i znowuż zajmuje mi możliwą do odnotowania chwilę, żeby zauważyć grę słów, to nie jest to moim zdaniem jedynie nierozruszanie umysłu, lecz coś już podpadającego pod jednostkę chorobową. Ale tytuły sobie zapisałem - jak nie teraz to chociażby później warto będzie zajrzeć.
immortal''' [ Pretorianin ]
brak wprowadzenia matmy obowiazkowej uwazam za jeden z glupszych pomyslow
© 2000-2024 GRY-OnLine S.A.

 --> Archiwum Forum
--> Archiwum Forum